JimYuan's Blog

Sharing the things I learned

0%

ConvexHull_Javis'_March

Posted on In , , , ,

Node

Introduction

I have implemented Convex hull algorithm in grasshopper by creating one C# scripting component. Here, I would like to note some codes I have learned.
There are many algorithms for finding convex hull, Javis' March, also known as Gift Wrapping Algorithm, should be the most intuitive one.
Though it is not the fastest one, this algorithm solve the problem with only an simple geometric algebra sense.

Some other algorithms about Convex hull can be found here

Dive into Algorithm

idea

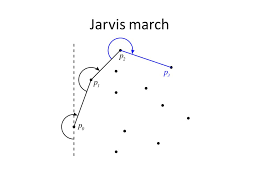
While marching, by the result of the cross Product to determine the next point.

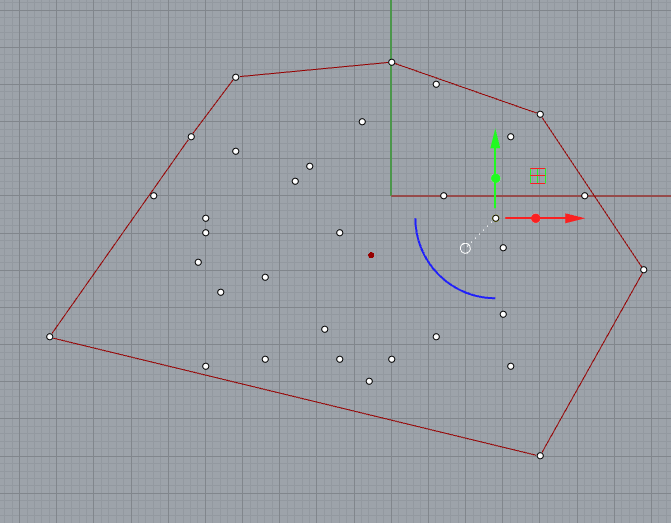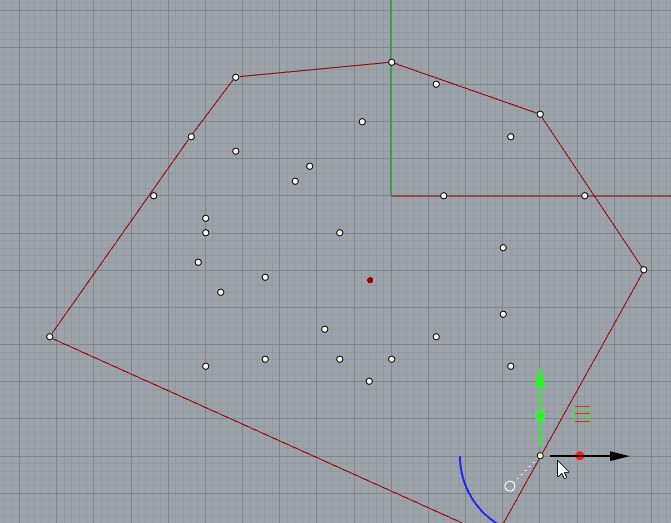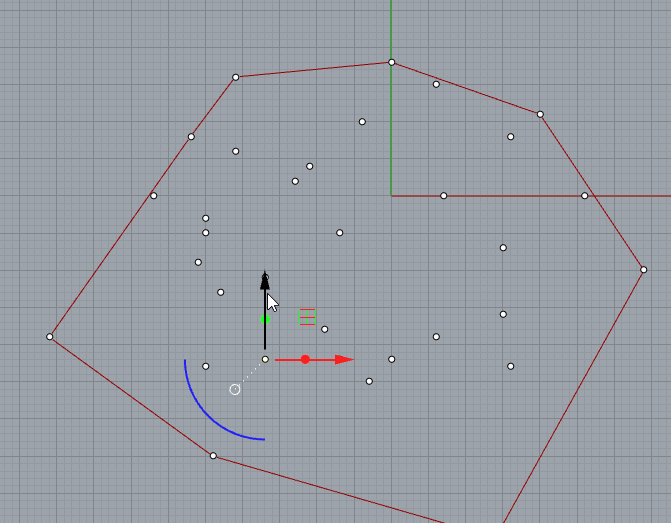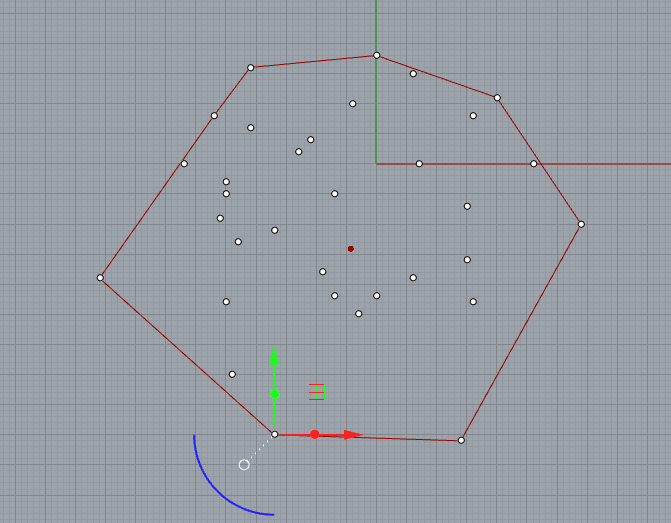
  • Prepare point cloud(many points) on one plane.
  • Decided the starting point
  • Using crossProduct property to march through the points.

Starting point

I set the buttom-most point as the starting point, and if the y is the same then compare x-value.

1
2
3
bool compare(Point3d a, Point3d b){ // to find the starting point
    return (a.Y < b.Y) || (a.Y == b.Y && a.X < b.Y);
}

CrossProduct

1
2
3
4
5
6
7
Vector3d crossProduct(Vector3d u, Vector3d v){
    double x = u.Y * v.Z - u.Z * v.Y;
    double y = u.Z * v.X - u.X * v.Z;
    double z = u.X * v.Y - u.Y * v.X;

    return new Vector3d(x, y, z);
}

Length2

Though we should calculate distance, which should use square root, we here can do the same thing without using it because we want the relationship, instead of the precise distance.
By doing this way, we get what we want, and because not using square root calculation, it is faster.

1
2
3
double length2(Point3d a, Point3d b){
    return (a.X - b.X) * (a.X - b.X) + (a.Y - b.Y) * (a.Y - b.Y);
}

All code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
private void RunScript(List<Point3d> pts, ref object A)
  {
    A = Javis_march(pts);
  }

  // <Custom additional code> 
  // find the buttom-most points(left most if the y values are the same)
  bool compare(Point3d a, Point3d b){
    return (a.Y < b.Y) || (a.Y == b.Y && a.X < b.Y);
  }

  Vector3d crossProduct(Vector3d u, Vector3d v){
    double x = u.Y * v.Z - u.Z * v.Y;
    double y = u.Z * v.X - u.X * v.Z;
    double z = u.X * v.Y - u.Y * v.X;

    return new Vector3d(x, y, z);
  }

  double length2(Point3d a, Point3d b){
    return (a.X - b.X) * (a.X - b.X) + (a.Y - b.Y) * (a.Y - b.Y);
  }

  bool far(Point3d o, Point3d a, Point3d b){
    return length2(o, a) > length2(o, b);
  }

  List<Point3d> Javis_march(List<Point3d> pts){

    List<Point3d> vertexs = new List<Point3d>();

    int start = 0;
    for(int i = 0; i < pts.Count;i++){
      if(compare(pts[i], pts[start]))
        start = i;
    }

    vertexs.Add(pts[start]);
    int current = start;

    do{
      int next = current;
      for(int i = 0; i < pts.Count; i++){
        double c = crossProduct(new Vector3d(pts[i] - vertexs[vertexs.Count - 1]), new Vector3d(pts[i] - pts[next])).Z;
        if(c > 0 || c == 0 && far(vertexs[vertexs.Count - 1], pts[i], pts[next])){
          next = i;
        }
      }
      vertexs.Add(pts[next]);
      current = next;
    }
    while(current != start);
    return vertexs;
  }

I used do-while first ,cause I want to at least run once, which make sure the list contains at least two points.

Note

Let’s assume if there are n points in the point cloud, and m points on the convex hull.
Then the total time complexity will be O(NM).

There are some faster algorithms doing sorting before running cross Product calculation, Andrew's Monotone Chain, for example. I might try to implement this algorithm the other day.

References