LinesIntersection_in_2D

Intersection in 2D

How to check if two given line segments intersect? (2D)
GeeksforGeeks
One can determine if two given line segments(2D/laid on the same plane) intersect by the Orientation.

Orinentation of an oedered triplet of points in the plane can be:

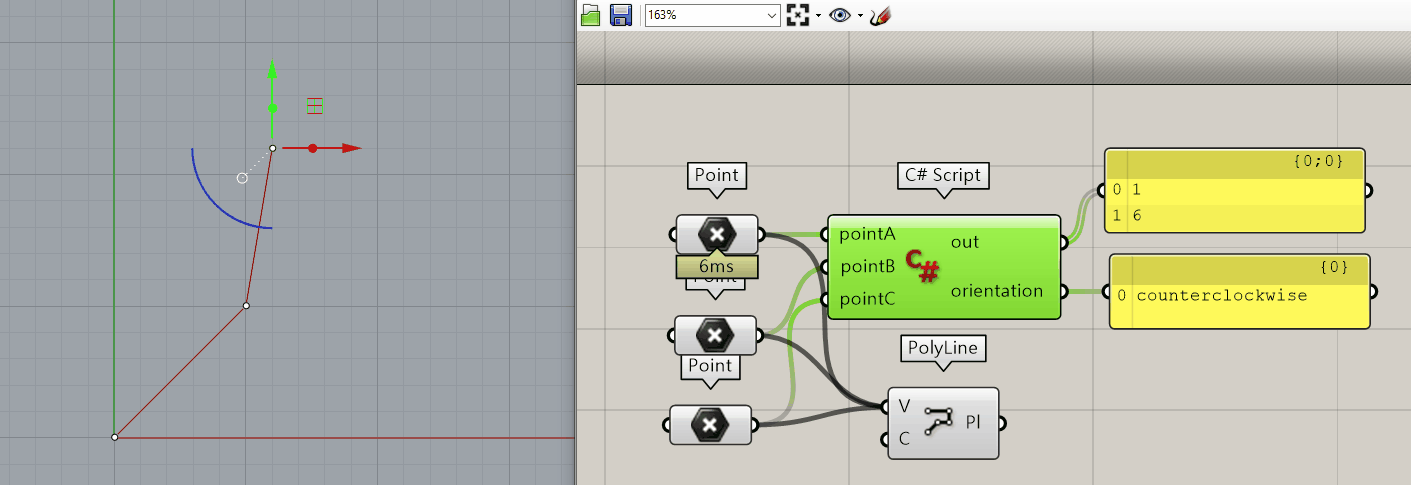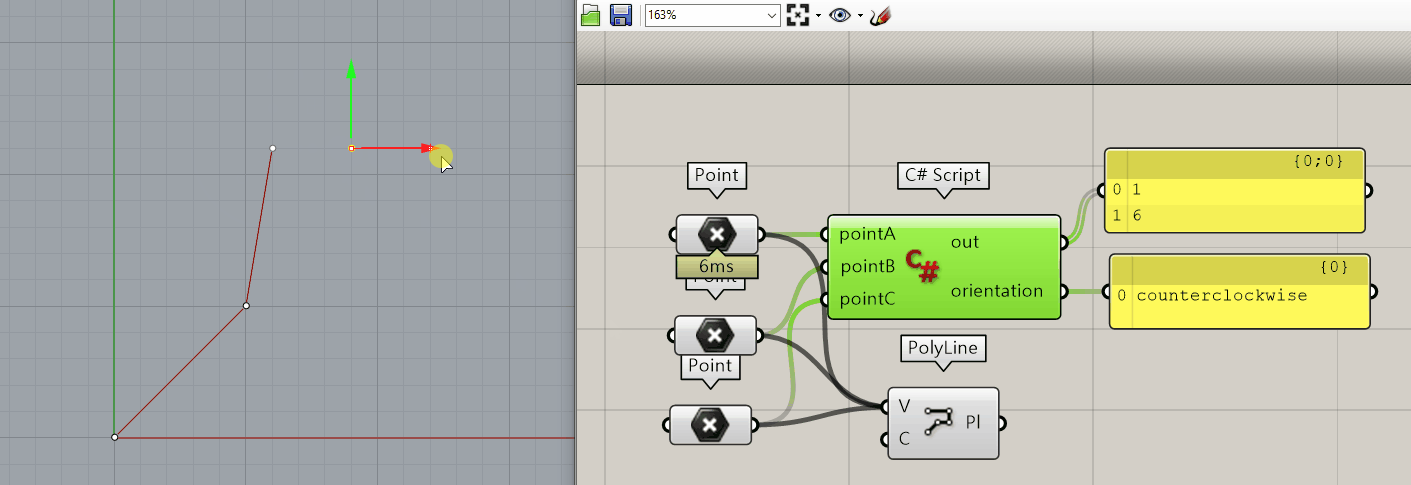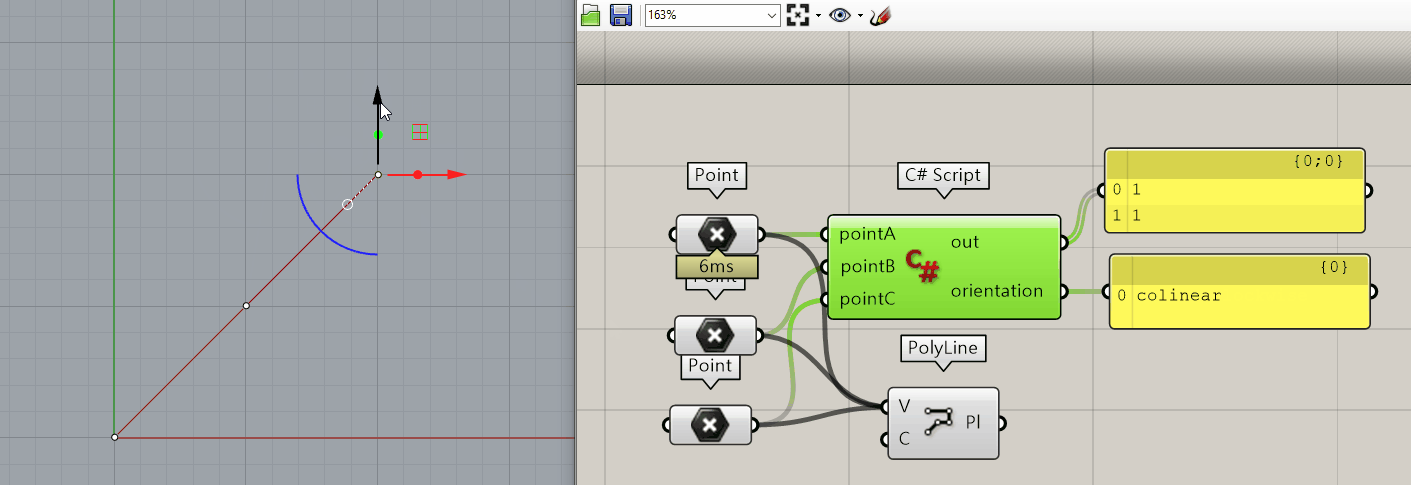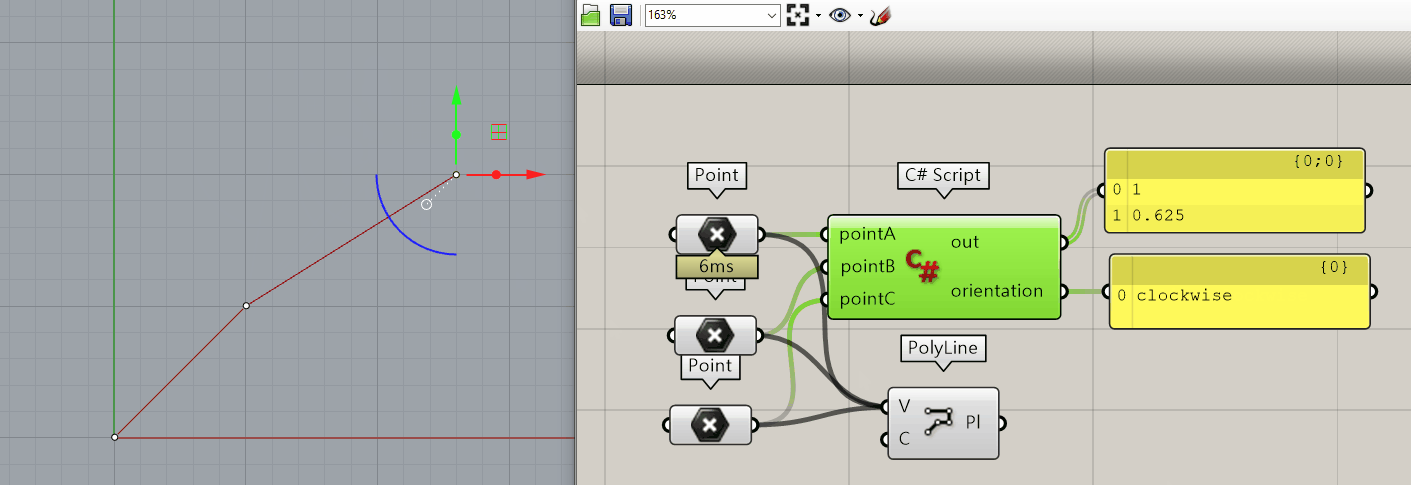
• counterclockwise
• clockwise
• colinear

Orinetation constructed by 3 points

check orinetation
In short, three points can form 2 lines. By checking these two lines($m_1$ & $m_2$) slope change, we can determine either

1. counterclockerwise($m_2>m_1$)
2. clockwise ($ m_2 > m_1$)
3. colinear ($ m_1 == m_2$)

private void RunScript(Point3d pointA, Point3d pointB, Point3d pointC, ref object orientation)
{
  double m1 = (pointB.Y - pointA.Y) / (pointB.X - pointA.X);
  double m2 = (pointC.Y - pointB.Y) / (pointC.X - pointB.X);

  Print(m1.ToString());
  Print(m2.ToString());
  if(m1 == m2) orientation = "colinear";
  else if(m1 > m2) orientation = "clockwise";
  else orientation = "counterclockwise";

}

Let’s assume there are two line segments Line A and Line B.

• The end points on Line A are Point p1 and Point q1
• The end points on Line B are Point p2 and Point q2
  as the picture shown below.
  Orientation of 3-ordered points

Example of lines intersect to each other

starting from Line A(p1)

$ p1 \rightarrow q1 \rightarrow p2$ is clockwise, while
$ p1 \rightarrow q1 \rightarrow q2$ is counterclockwise.

starting from Line B(p2)

$ p2 \rightarrow q2 \rightarrow p1$ is counterclockwise, while
$ p2 \rightarrow q2 \rightarrow q1$ is clockwise.

If both cases have different orientations, then we can say that they are intersected to each other.

Example of lines are not intersected

starting from Line A(p1)

$ p1 \rightarrow q1 \rightarrow p2$ is clockwise, while
$ p1 \rightarrow q1 \rightarrow q2$ is counterclockwise.

starting from Line B(p2)

$ p2 \rightarrow q2 \rightarrow p1$ is counterclockwise, and
$ p2 \rightarrow q2 \rightarrow q1$ is also counterclockwise.

Special Case - colinear

Two lines colinear